![0.Romeo_And__Juliet-_Dang_cap_nhat_[NCT_8316951878].mp3](https://d2.violet.vn/uploads/thumbnails/document/0/329/643/0.Romeo_And__Juliet-_Dang_cap_nhat_[NCT_8316951878].mp3.jpg)
Chào mừng quý vị đến với website của Lê Na
Nếu chưa đăng ký, hãy nhấn vào chữ ĐK thành viên ở phía bên trái, hoặc xem phim hướng dẫn tại đây
Nếu đã đăng ký rồi, quý vị có thể đăng nhập ở ngay phía bên trái.
Giờ các nước
CAUCHY(CÔ SI)
Augustin Louis Cauchy
 Augustin Louis Cauchy |
|
| Sinh | 21 tháng 8 năm 1789(1789-08-21) Paris, Pháp |
|---|---|
| Mất | 23 tháng 5 năm 1857 (67 tuổi) Sceaux, Pháp |
| Nơi ở |  Pháp |
| Quốc tịch | Pháp |
| Ngành | Calculus Complex analysis |
| Học trường | Trường Bách khoa Paris |
| Các sinh viên nổi tiếng | Francesco Faa' di Bruno |
| Nổi tiếng vì | Tích phân Cauchy |
| Tôn giáo | Catholic[1] |
Augustin Louis Cauchy (đôi khi tên họ được viết Cô-si) là một nhà toán học người Pháp sinh ngày 21 tháng 8 năm 1789 tại Paris và mất ngày 23 tháng 5 năm 1857 cũng tại Paris. Ông vào học Trường Bách khoa Paris (École Polytechnique) lúc 16 tuổi. Năm 1813, ông từ bỏ nghề kỹ sư để chuyên lo về toán học. Ông dạy toán ở Trường Bách khoa và thành hội viên Hàn lâm viện Khoa học Pháp.
Công trình lớn nhất của ông là lý thuyết hàm số với ẩn số tạp. Ông cũng đóng góp rất nhiều trong lãnh vực toán tích phân và toán vi phân. Ông đã đặt ra những tiêu chuẩn Cauchy để nghiên cứu về sự hội tụ của các dãy trong toán học.
Bất đẳng thức Cauchy
Bách khoa toàn thư mở Wikipedia
Trong toán học, bất đẳng thức Cauchy, bất đẳng so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm được phát biểu như sau:
- Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
- Với 2 số:
-
- Đẳng thức xảy ra khi và chỉ khi a = b
- Với n số:
-
-
-
- Đẳng thức xảy ra khi và chỉ khi
-
![\frac{x_1 + x_2 + ... + x_n}{n} \geq \sqrt[n]{x_1.x_2. ... .x_n}](http://upload.wikimedia.org/math/0/f/7/0f7b4ad63905b541aa31244dd6474466.png)
Tổng quát hóa
Trung bình có hệ số
Cho n số x1, x2, ..., xn ≥ 0
và các hệ số α1, α2, ..., αn > 0.
Đặt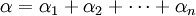 
.
Bất đẳng thức trung bình cộng và trung bình nhân cũng đúng nếu hai giá trị trung bình có hệ số, như sau:
![\frac{\alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n}{\alpha} \geq \sqrt[\alpha]{x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_n^{\alpha_n}}](http://upload.wikimedia.org/math/d/7/2/d7285ff8e6f3ba98e1dc0934631c1c20.png)
Đẳng thức khi và chỉ khi 
Với các loại trung bình khác
Trung bình điều hòa ≤ trung bình nhân ≤ trung bình cộng
![\frac {n} {\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n}} \leq \sqrt[n]{x_1x_2...x_n} \leq \frac{x_1+x_2+...+x_n}{n}](http://upload.wikimedia.org/math/6/c/8/6c8769d5aba505f331d67f99ed739a94.png)
Đẳng thức khi và chỉ khi
Nguyễn Thị Lê Na @ 20:59 01/06/2012
Số lượt xem: 722
TIN NHẮN